
This work describes a method for reconstructing water-tight surfaces from an input of oriented points. It shows that the surface reconstruction algorithm presented by the FFT method can be expressed as a solution to a Poisson equation. Thus, by adapting an octree to the point set and solving the Poisson equation on the octree (rather than on a regular voxel grid) the algorithm provides a method for reconstructing much higher resolution models without incurring the prohibitive memory overhead exhibited by prior methods.
The latest version also supports the incorporation of point constraints as a screening term, allowing for the reconstruction of more detailed surfaces within the same adapted Poisson framework.
(SGP 2006, ToG 2013, CGF 2018, SGP 2020, CGF 2023)
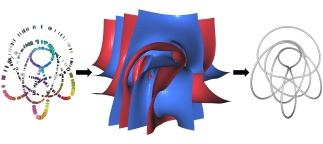
This work provides an extension of the standard Poisson Reconstruction algorithm that supports reconstruction of manifolds with co-dimension larger than one from framed samples. The approach computes a multi-valued implicit function by formulating the reconstruction problem as a multi-linear optimization problem expressed in terms of the exterior products of the gradients of the function and returns the zero level-set of the multi-valued function.
(SGP 2023)

This work provides a way for computing finite-element basis functions on polygonal and polyhedral domains. In addition to defining the basis functions, it provides applications including simulation of linear elasticity, numerical evaluation via the Franke test, geodesic computation using the Heat method, gradient-domain smoothing/sharpening of signals on the surface, and visualization of tangent vector fields through line-integral convolution.
(SIGGRAPH 2022)
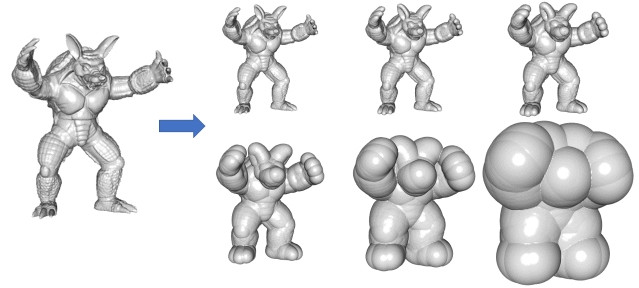
This code provides implementations of the Euclidean Distance Transformation described in [Danielsson, 1990] and [Saito and Toriwaki, 1994]. The former produces higher quality results due to its use of sub-voxel distance sampling. The latter computes distances at voxel precision (i.e. after rasterizing the mesh into a binary grid) but is noticeably faster.
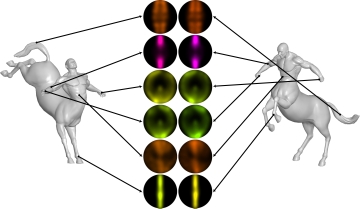
This work provides a way for computing highly distinctive and robust local surface feature descriptor. An intrinsic signal and frame is associated with every point on the mesh. Then, the descriptor at a feature point is obtained by having each of the feature point's neighbor vote into the bin corresponding to the position of the feature point within the frame of the neighbor, with a weight equal to the value of the signal at the neighbor's position.
(CGF 2021)
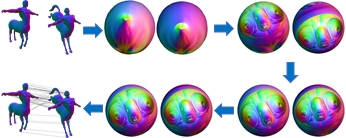
This work provides a way for computing dense point-to-point correspondences between two genus-zero surfaces by decomposing the processing into a per-model parametrization phase and a per-pair-of-models registration phase. In the parametrization phase surfaces are conformally mapped to the sphere, Möbius centered to remove ambiguity due to inversions, and authalically evolved to make the scale factors uniform. In the registration phase the surfaces are initially aligned for rotation and the alignment is then refined using optical flow.
(SGP 2019)

This work provides a way for performing gradient-domain processing of signals represented over surface in 3D. To this end, we define finite-elements systems in texture spaces, addresing the problems of (1) metric-awareness and (2) cross-seam continuity. The advantages of this approach are two-fold. First, it enables the processing of texture maps without re-sampling to mesh vertices. Second, the regularity of the texture-spacde presentation enables an efficient hierarchical solver that supports processing of high-resolution textures at interactive frame-rates.
(SIGGRAPH 2018)

This work shows that the Moebius transformation registering two surfaces can be found efficiently. Breaking the transformation into two parts, inversion and rotation, we address the registration problem by handling these components separately. For inversion, we provide a new technique that canonically poses the parameterization. For rotation, we leverage earlier work on efficient spherical correlation to find the optimal alignment.
(SGP 2018)
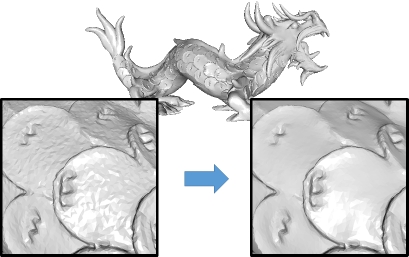
This work extends the classical image-based gradient-domain processing paradigm to the processing of signals on meshes, supporing the Laplacian smoothing/sharpening of color values and vertex positions. By formulating the Poisson equation in an intrinsic manner that only depends on the per-triangle metric tensor, the implementation supports edge-aware filtering by allowing the user to adjust the metric tensor using an esimate of the total curvature.
(SGP 2009), (SIGGRAPH 2016), (JCGT 2016)

This work extends the classical image-based optical flow comptuation to support processing of textures/signals on meshes. The code provides an application for interpolating between source and target textures/signals. Given the source and target, we compute the vector field whose forward flow takes the source to the target and whose backward flow takes the target to the source. We then define the in-between texture/signal at time τ∈[0,1] by flowing the source forward for time τ, flowing the target backward for time 1-τ, and then cross-disolving the advected textures/signals using weights 1-τ and τ.
(SIGGRAPH 2016)

This work provides an approach for performing color-correction of 3D EM data. The processing is decomposed into two phases: An initial smoothing pass to obtain a 3D dataset that is coherent along the z-axis, followed by independent 2D gradient domain fusion to obtain slices that preserve the high-frequency content of the input slices while exhibiting the coherence of the smoothed data. Separating the color correction into these two phases makes the approach trivially parallelizable anb provides the space- and time-efficiency required for processing large 3D volumes.
(ArXiv 2015)
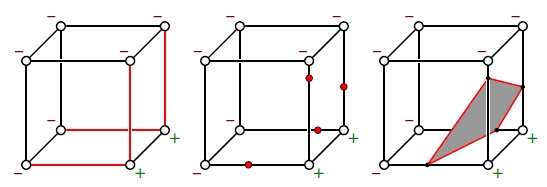
This work provides an extended implementation of the classical Marching-Cubes algorithm, supporting a full-case table for resolving ambiguities, polygon / minimial-area-triangulation output, and Hermite data interpolation.
(3DV 2015)
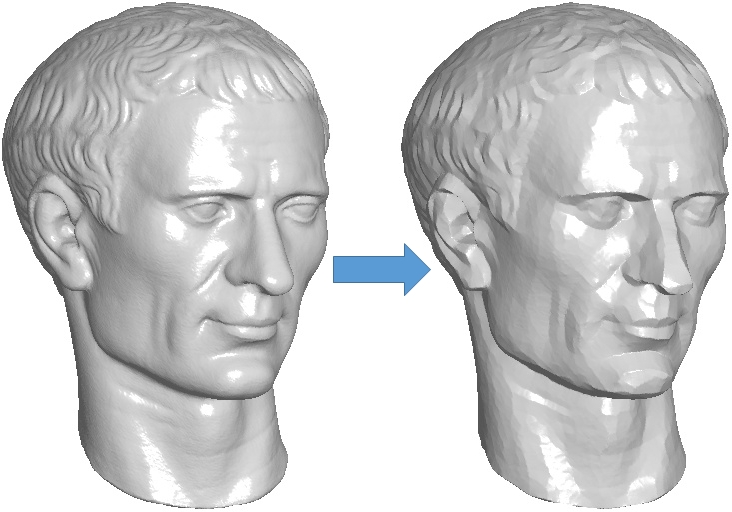
This work revisits the Shock Filters proposed by Osher and Rudin (1995) and shows how the PDE can be interpreted as the advction of the input signal. We show how this interpretation facilitates the theoretical analysis of the processing, as well provide extensions to the processing of signals on triangle meshes. Applying the technique to the normal field, we obtain a simple technique for mesh-sharpening.
(SGP 2015)

This work considers the problem of solving linear systems on geometries with symmetries. In particular, when the linear system commutes with the symmetry group, the decomposition of the function space into irreducible representations results in a block-diagonalization of the matrix, replacing the solution of one large system with the solutions of many small ones. For Poisson equations on surfaces of revolution, the decomposition into irreducibles is obtained by computing a set of FFTs along the parallels of the surface, and the diagonal blcoks are tri-diagonally banded so that they can be solved in linear time.
(SGP 2015)

This work presents a modification to the traditional mean-curvature flow that appears to evolve genus-zero surface to conformal mappings onto the unit sphere. By adapting the flow to use a conformalized metric, the flow avoids the numerical instabilities arising in implementations of the traditional flow, slowing down the evolution in cylindrical regions to allow the surface to evolve without forming neck-pinches.
We further adapt the approach to compute conformal spherical orbifold embeddings of sphere- and disk-like surfaces by introducing symmetry constraints within the lienar system.
(SGP 2012)
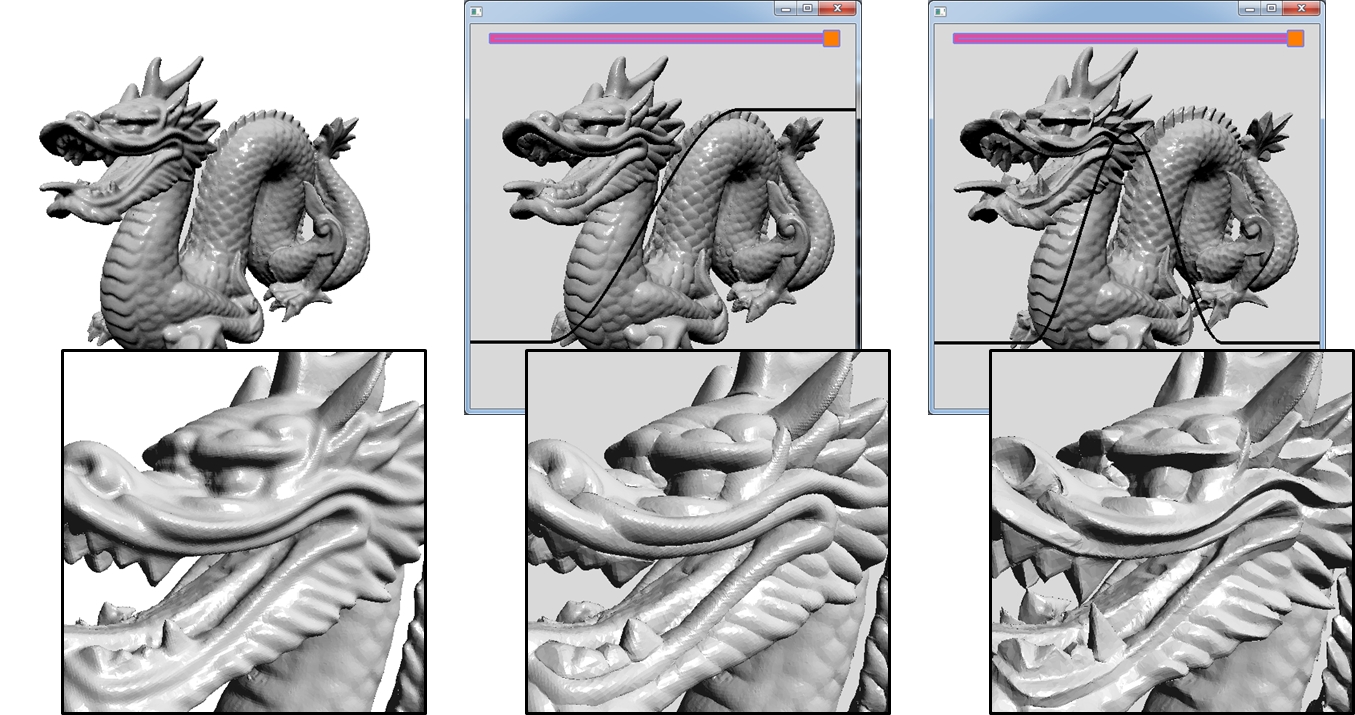
This work develops an approach for performing anisotropic geometry processing. Formulating geometry processing as the solution to a screened Poisson equation, using an efficient multigrid solver to solve the linear system, and using piecewise-constant elements to represent the anisotropic scale, we support the editing of large meshes at interactive rates.
(SIGGRAPH 2011)
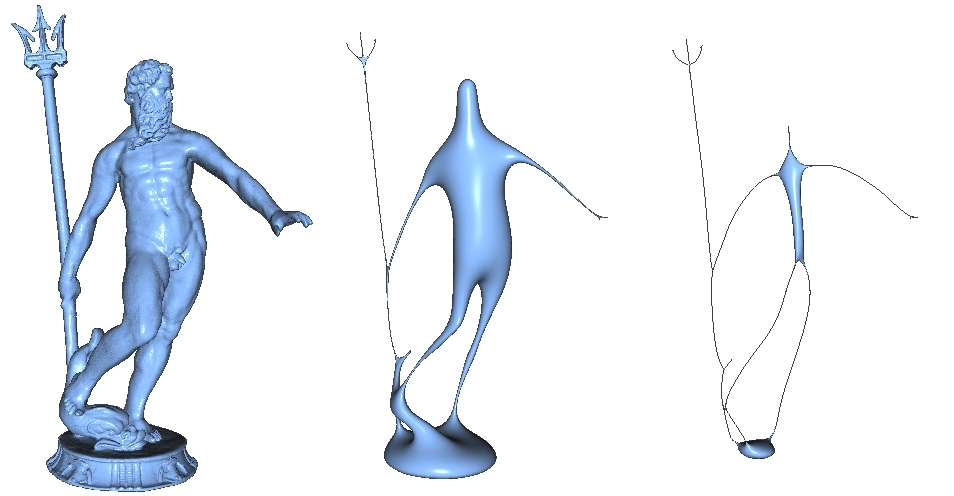
This work develops an approach for efficiently evolving meshes using mean-curvature flow. Using an octree-based finite-elements system, we track the flow of quadrature points and their Jacobians in order to be able to correctly define the Poisson system over the evolved geometry.
(CGF 2011)

This work develops a metric-aware, streaming multigrid solver for efficiently processing equirectangular spherical images. The solver uses the symmetry of the parameterization to efficiently define the linear system and hierarchicaly adapts the tesselation of the sphere near the poles to ensure that the linear system remains well-conditioned.
(SIGGRAPH Asia 2010)
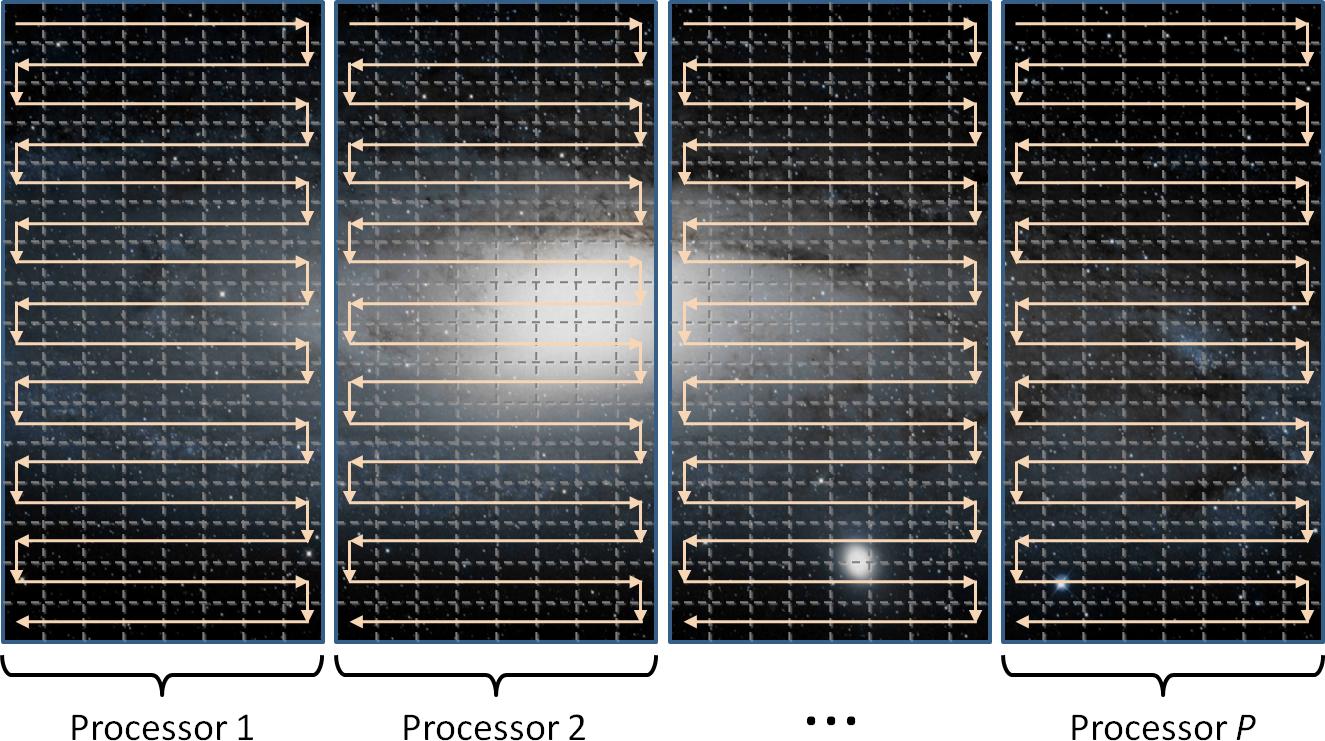
This work develops a distributed and streaming multigrid solver to efficiently process large planar or spherical images. The solver partitions images into bands, streams through these bands in parallel within a networked cluster, and schedules computation to hide the necessary synchronization latency. Using the solver, we can process images ranging from tens of millions up to one-trillion pixels.
(ToG 2010)
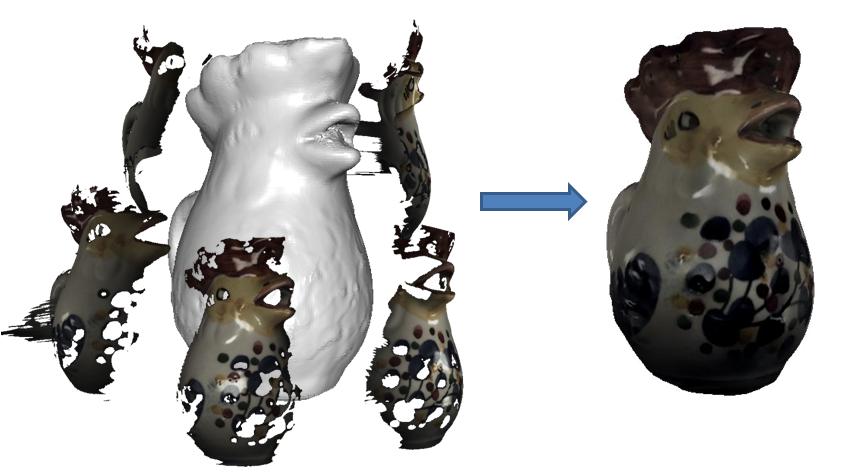
This work explores a new formulation of finite-elements over meshes. By considering the reconstruction of 3D elements defined over a voxel grid to the suface of the mesh, we can define a function space that inherits the regularity of the voxel grid, facilitating the design of a multigrid solver for solving the Poisson equation.
(SGP 2009)

This work introduces a new tool for solving the large linear systems arising from gradient-domain image processing. It develops a streaming multigrid solver, which needs just two sequential passes over out-of-core data. The resulting system can solve the huge linear systems associated with performing stitching and tone-mapping on gigapixel images while maintaining a small in-core memory footprint. Due to its fast convergence and excellent cache behavior, the streaming solver is also efficient for in-memory images.
(SIGGRAPH 2008)

This work describes an out-of-core method for performing Poisson surface reconstruction. We introduce a novel multilevel streaming octree representation that enables solving the global reconstruction problem by performing only three passes through the data. Since each pass only requires that local data is maintained in core, our approach provides a method for reconstructing surfaces when the initial point set, the output mesh, and the intermediate data structures are themselves too large to fit into working memory.
(SGP 2007)
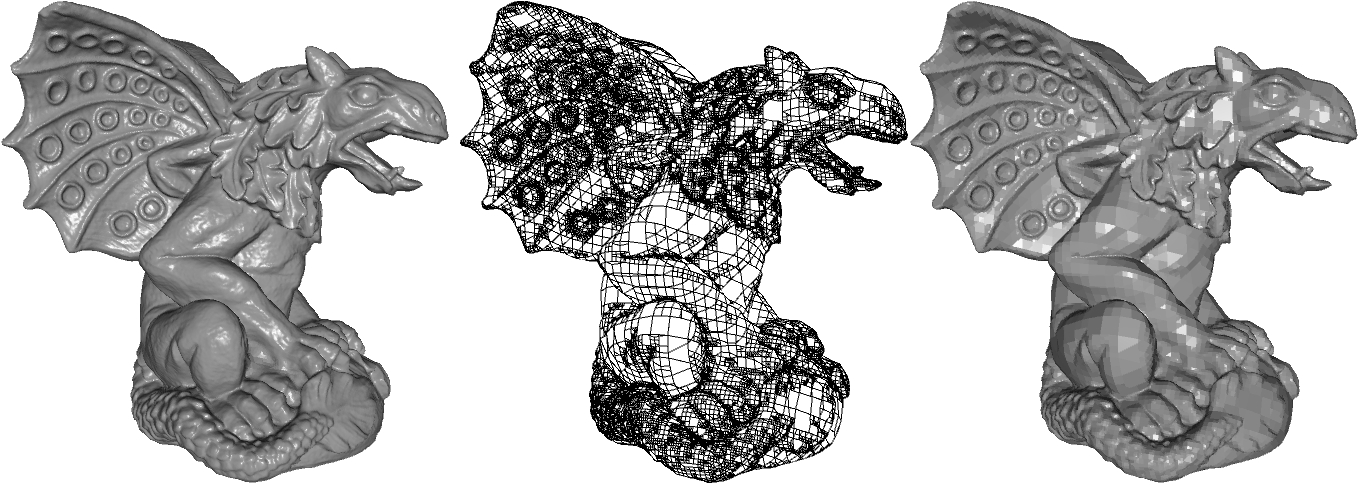
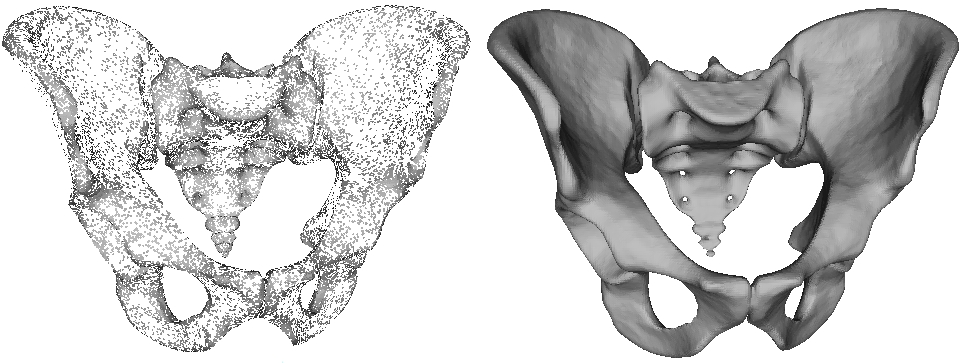
This work describes a method for extracting a watertight surfaces from an octree representation of an implicit function. Using the topology of the octree to define a set of binary edge-tree, the work shows that inconsistencies due to depth disparities between adjacent leaf nodes can be resolved, and a watertight isosurface can be extracted without restricting either the topology or the values associated to the octree.
(SGP 2007)
This work describes a method for reconstructing water-tight surfaces from an input of oriented points. The method reduces the problem of surface reconstruction to convolution, and provides an efficient method for reconstruction that reduces the reconstruction process to three simple steps: (1) splatting the oriented points into a voxel grid, (2) efficiently convolving with a fixed filter using the FFT, and (3) extracting an iso-surface use marching cubes. The additive nature of the reconstruction makes it stable in the presence of noise, and a simple heuristic allows to work well when the points are non-uniformly distributed.
(SGP 2005)

This work describes a method for efficiently computing the symmetries of a model with respect to every axis passing through the model's center of mass. The SGP '04 paper describes how fast signal-processing over S^2 and SO(3) can be used to compute the symmetry descriptors, and describes how the symmetry values can be used to improve retrieval performance.
(SGP 2004)
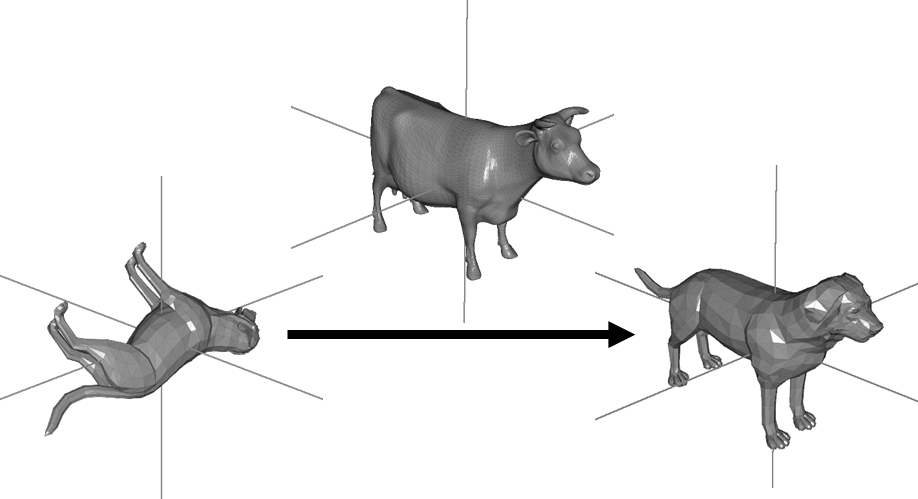
This work presents an approach for registering two 3D models by representing each one by an implicit function in 3D and using the fast spherical harmonic transform and fast Wigner-D transform to compute the correllation between the. invariant representations of 3D shapes. The SIGGRAPH '04 paper describes an application of this approach in the context of modeling by example. performance.
(SIGGRAPH 2004)
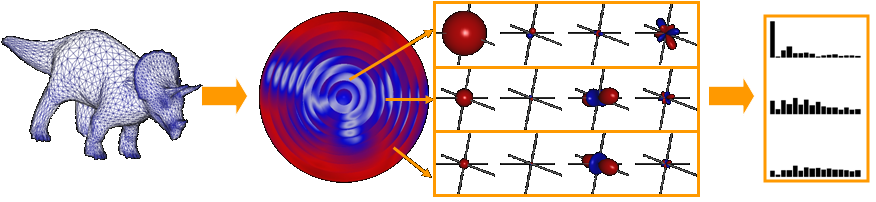
This work considers the limitations of canonical alignment and presents a new mathematical tool, based on spherical harmonics, for obtaining rotation invariant representations of 3D shapes. The SGP '03 paper describes the properties of this tool and shows how it can be applied to a number of existing, orientation dependent, descriptors to improve their matching performance.
(SGP 2003)
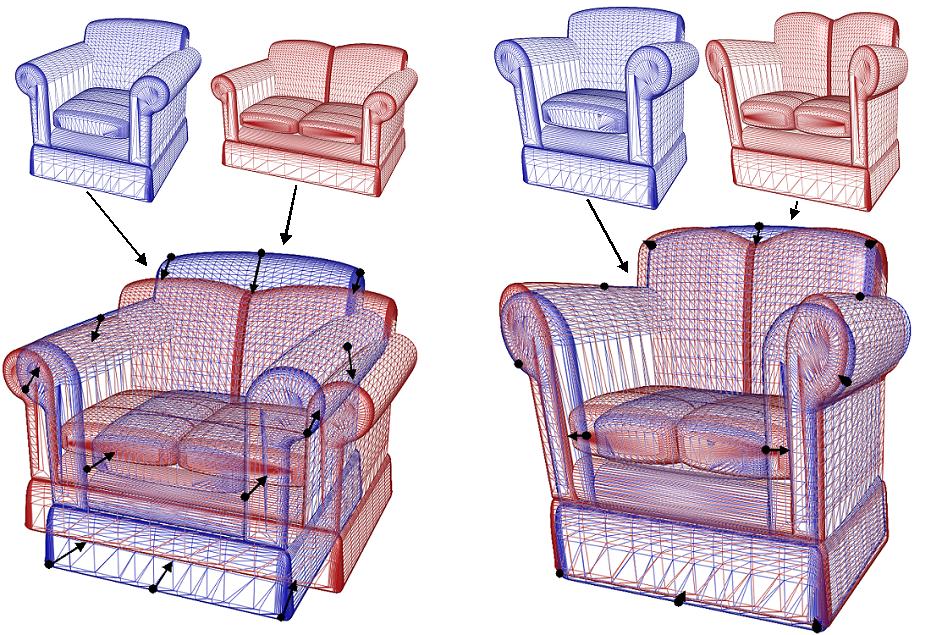
This work describes an iterative method for transforming anisotropic models (models whose surface point variance is a function of direction) into isotropic models (models whose covariance matrix is a constant multiple of the identity matrix). The SIGGRAPH '04 paper describes applications of anisotropic factorization to the domain of shape matching, where classes of models that vary across anisotropy are difficult to match, due to the fact that often the wrong correspondences are established between points on the two surfaces.
(SIGGRAPH 2004)