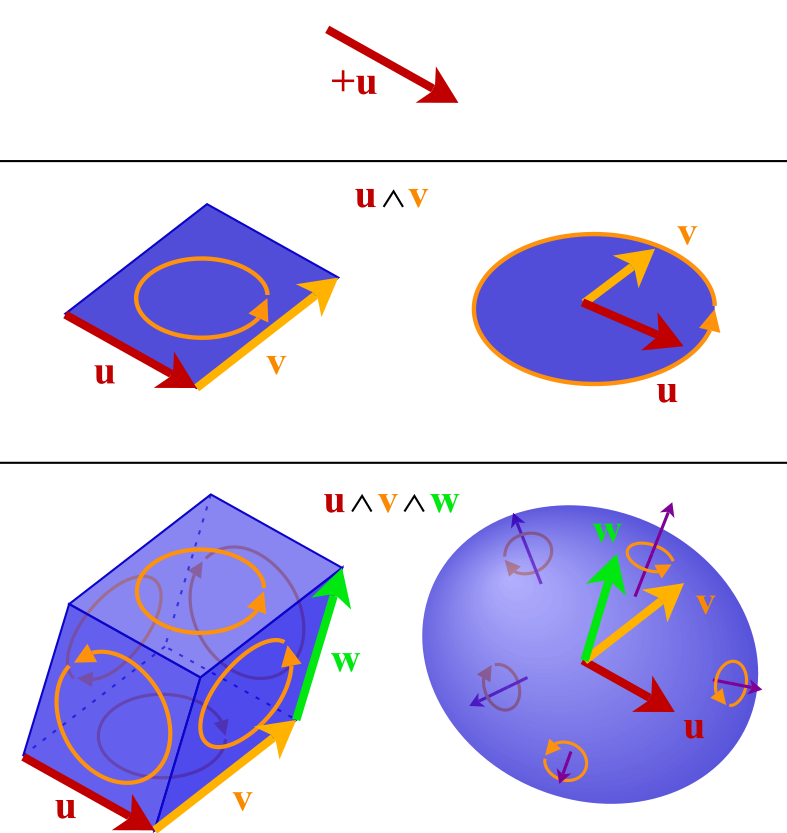
Geometric Algebra (GA) is an extension of Linear Algebra, popularized by the physicist David Hestenes. Linear Algebra manipulates one-dimensional objects, the vectors, using only algebraic expressions and without referencing a coordinate system; Geometric Algebra generalizes this concept to manipulate higher dimensional objects algebraically and without defining the objects in coordinate systems. As a result, GA provides a unified mathematical language to model various kinds of problems across different areas, including physics (special and general relativity), computer sciences (computer graphics), engineering (robotics), etc.

This course is for freshmen who have no background in Linear and Geometric Algebra. We will begin with tutorial and hands-on in-class exercises to explore Compass Ruler Algebra. Then, we will learn the mathematical foundations of GA, starting with 2D Euclidean geometry that students should have learned in high school, and extend the concept to Compass Ruler Algebra. At last, we will study its applications in robot kinematics, computer vision, and computer graphics.