600.226 Data Structures (Spring 2004 - Prof. Eisner)

Homework 6 ... due 4pm Tuesday 23 Mar 2004 (just after spring break)

This page and the provided source files are based on the 3nd edition of the textbook. Use this page if possible (it's definitely better), but you may instead continue to use the old 2nd-edition version if you've already started working on that. The two versions differ somewhat in the terminology, the Java interfaces, and the provided source code.

Summary

Goal of this homework: This is the first part of a longer assignment on election systems. You will implement a heap-based adaptable priority queue (with comparators and location-aware entries), more or less as described in the book. You will then apply it to real voting data that you read from a file.

The next two assignments will extend this work. By the end, you will have built a complicated system with several interacting data structures.

Collaboration policy for this homework: You must follow the CS Department Academic Integrity Code, except that for this homework, you may optionally work with one other student in the class. If you do so, you must say who your partner was at the top of your Readme file, and both of you will receive the same grade for the assignment.

How to hand in your work: instructions, upload page

What to hand in (all packaged up in a zip or tar file):

Acknowledgments: Thanks to Usman Zaheer and Yuan Chen for their help in preparing this assignment.

Introduction

As discussed in class, a priority queue keeps track of what to do next. Examples:

Answer the following in your Readme file:

  1. In the Palm Pilot example, the "reminder queue" must support three operations: CHECK whether there is an appointment 10 minutes from now or less, ADD a new appointment to the queue, DELETE an appointment from the queue once the reminder has been delivered.

    1. Why wouldn't an ordinary queue be an appropriate implementation of a reminder queue?
    2. If you implement the reminder queue using a priority queue, what are the keys and values? What is the comparison function on keys?
    3. What priority queue method do you call for each of the three operations CHECK, ADD, and DELETE?
    4. Which of these three operations needs to be fast for this application?
    5. What implementation would you pick for the priority queue in this circumstance: sorted sequence, unsorted sequence, or heap? Explain carefully why your answer is better than both of the other answers.

  2. This assignment will deal with the city council election example. We will indeed construct a priority queue of all candidates, as described above, for reasons that will become clear later. But if we had 1,000,000 candidates for the 9 seats, this priority queue would be quite big and slightly slow. Briefly sketch a more efficient method that does exactly the same thing - prints out the top 9 candidates from best-to-worst order - using only a small priority queue and a small stack. (We developed most but not all of the answer in class.)

Testing a Heap-Based Priority Queue

Download all the source code we are giving you. You can download the files one at a time, or get it all at once in a zip file.

Your first job is simply to try out a heap-based priority queue, as discussed in the book and in class. The priority queue will implement the following interface:

public interface PriorityQueue {
  public int size();
  public boolean isEmpty();
  public Entry insert(Object key, Object value) throws InvalidKeyException;
  public Entry min() throws EmptyPriorityQueueException;
  public Entry removeMin() throws EmptyPriorityQueueException;
}

We are providing you with the full HeapPriorityQueue class that is defined in the book, as well as the class that it is based on, VectorCompleteBinaryTree (which implements CompleteBinaryTree).

You will have to make a couple of changes to the code at this point. The VectorCompleteBinaryTree class won't compile as given, because it is written to use the Vector interface developed in the textbook. You should trivially fix it to use Java's standard java.util.Vector class (you'll want to click that link to read the class documentation). Once you've done that, it should compile.

Read the code for these classes and interfaces. You are expected to understand it for the midterm. Moreover, later in the assignment you will be required to modify this textbook code to make it more efficient! The interface won't change, just the implementation.

A few remarks:

Answer the following in your Readme file:

  1. The BinaryTree interface and its extension CompleteBinaryTree do not require you to support createExternal(). Remember that your LinkedBinaryTree class in homework 5 did support that method.

    You could find a way to implement createExternal() in VectorCompleteBinaryTree, too ... but it's probably a bad idea. An application like arithmetic expression parsing (homework 5), which needs to make arbitrary calls to createExternal(), should probably not be using VectorCompleteBinaryTree. Why not? (Hint: Think about space efficiency as well as time efficiency.)

Write a test method to check that HeapPriorityQueue class works correctly. The Election class that you will write below will help you test it, too, but it may not provide a complete test (unless you write your own ballots file). I recommend writing a short main(String[] args) method that sorts args (i.e., the strings specified on the command line). As it inserts each string, it can print out the minimum string so far. Then it can remove them all from the priority queue to print them in sorted order. When you make the code more efficient, below, you can use the same test method to make sure it still works correctly. The graders will also test your code.

Election Data

Everyone now knows how important it is to count the votes correctly. In the aftermath of Bush v. Gore and their hanging chads, computer scientists have been important figures in thinking about the design of election equipment (or Internet voting) that is as resistant as possible to error and fraud.

Computer scientists (along with economists) also like to think about alternative voting systems. In this and subsequent assignments, we will be working with real data from the 1999 City Council election in Cambridge, MA. Like Ireland and Malta and many professional societies, Cambridge uses an interesting alternative voting system that we will deal with in homework 8.

For this assignment, we'll just count the votes in the usual way. There were 24 candidates for 9 seats in the election. So you will end up with a heap of size 24, which is large enough to test your code.

Your data are in the file ballots, which contains nearly 19,000 ballots. Download it. The candidates are numbered from 1 to 24, and each ballot is represented by a single line with the number of the selected candidate. Here are the names of the candidates in an array for you:

  private static final String[] CANDIDATES = { 
    null,    // there is no candidate 0
    "Born", "Braude", "Chase", "Christenson", "Davis", "Decker", 
    "Dixon", "Galluccio", "Giacobbe", "Goodwin", "Hoicka", "Jones", 
    "Maher", "Nidle", "Peixoto", "Reeves", "Snowberg", "Sullivan", 
    "Toomey", "Triantafillou", "Trumbull", "Williamson", "Winters", "Wormwood-Malone" 
  };

You should write an SimpleElection class with an appropriate main() method so that

java SimpleElection 9 ballots
will read in the ballots file and print out the names of the 9 council-seat winners, in order, starting like this:

(2730 votes) Candidate 8: Galluccio
(1669 votes) Candidate 1: Born
(1653 votes) Candidate 6: Decker
...
(These totals differ slightly from the official election totals
because of issues with invalid ballots and write-in candidates.)

You will use the HeapPriorityQueue class to sort the candidates into order (winner first). The easiest overall solution is to start by counting up each candidate's total and storing it in an array or java.util.Vector. Once you have done this, you can insert all the candidates into your heap, as discussed in the assignment introduction, and proceed in the obvious way. The elements on your heap can be candidate names or numbers, as you prefer.

Try to observe good style. It is bad style for your SimpleElection class to consist of a single main() function. You should break it up into logical units. It would also be bad style to make all your methods static. You should allow for the possibility of many SimpleElections going on at once. Ask yourself: What kind of data should be maintained by a SimpleElection object? What are the natural methods to update and access these data during an election?

We will be gentle about testing your code this week, but it is good to try to anticipate and handle any weird conditions and exceptions that may arise. In next week's assignment you will be expected to make this code very robust. You should also worry about which methods are public. After all, elections need to be both error-proof and tamper-proof!

Caution: Of course, your program should not be specialized to the number 9 or the filename ballots; it should get them from the command-line arguments that are passed to main(). In particular, you should be able to handle any number of candidates, numbered 1 through n. It is true that the CANDIDATES array we gave you above only holds 24 names, so for candidates 25 and up (if n > 24) you should just use an empty string for the name: that is, just print "Candidate 25: ". The CANDIDATES array is just a hack that we'll fix in next week's assignment (when the ballot format will change to specify names directly, not numbers).

Hint: A web search will turn up lots of help on Java file I/O. Here is a short lesson on how to read from a file in Java, among other things. (It has one error: parseInt() in one place is incorrectly written as parseInteger().)

Hint: By default, your heap will use a DefaultComparator that compares Integers in the usual way -- so the candidate with the fewest votes will end up on top of the heap. You will need to write your own comparator that orders the vote counts in the opposite way. How? That's for you to figure out, but here are a few other comparator classes that might inspire you.

// Uses the "natural order" on objects by calling their own compareTo methods.
// (A copy of this appears in HeapPriorityQueue as an inner class.)
public class DefaultComparator implements java.util.Comparator {
  public int compare(Object a, Object b) { return ((Comparable) a).compareTo(b); }
}

// Like DefaultComparator, but specialized to Integers.
public class DefaultIntegerComparator implements java.util.Comparator {
  public int compare(Object a, Object b) { return ((Integer) a).compareTo(b); }
}

// Does the same thing as above, but more directly (without calling compareTo()).
public class IntegerComparator implements java.util.Comparator {
  public int compare(Object a, Object b) { return (Integer)a - (Integer)b; }
}

// Wraps an existing comparator to make another comparator with related behavior.
// You might find this wrapping technique useful in reversing an existing comparator,
// such as DefaultComparator.
//
// In this case, we are wrapping an existing comparator that cannot compare null,
// with a new comparator that treats the special key null as less than everything else --
// essentially, as negative infinity.  It can be handy to have such a key.

public class NullComparator implements java.util.Comparator {
  java.util.Comparator c;   // the original comparator
  public NullComparator(java.util.Comparator c) { this.c = c; }
  public int compare(Object a, Object b) { 
    if (a==null) return (b==null ? 0 : -1);  // null is less than everything but null
    else if (b==null) return 1;              // everything else is greater than null
    else return c.compare(a,b);              // if neither is null, use original comparator
  }
}

Improving the Code

There are several things that can be improved in the book's HeapPriorityQueue and VectorCompleteBinaryTree code. Please fix them as follows. This should not affect the results of the election at all, nor should it affect the results of the test method (main()) that you wrote earlier. So you can keep re-testing after each change, to make sure everything still works.

Improving HeapPriorityQueue

Improving VectorCompleteBinaryTree

Reprioritization and Deletion on a Priority Queue

[Note: This section is all explanation. Just read it, as you would read the textbook or a handout, and answer the questions in your Readme. The next section will ask you to implement this design.]

Motivation

The introduction to this assignment gave 3 example applications of a priority queue. Let's think about those applications some more:

Alas, the basic PriorityQueue interface doesn't let you manipulate entries that are not at the front of the priority queue. So it doesn't support reprioritization (a change to an entry's key), or deletion (removal of the entry).

No object-oriented solution to this problem was published until 1999, in a paper by Goodrich and Tamassia, the authors of the textbook. That should prove to you that quite basic innovations in data structures are still possible -- an undergrad like you could have thought of this one! Section 7.4 of the book describes how to extend PriorityQueue to solve this problem, using "location-aware entries."

As a design lesson, this section will take you through the steps that lead to the invention of location-aware entries. As usual, there is no magic here, just repeated revision of the design to solve the problems that may come up.

Changing an Entry in the Adaptable Priority Queue

Remember that the elements stored at the nodes of the CompleteBinaryTree are "entries," each of which is a (key,value) pair. If we can find the Entry that we want to change, we can easily change it in any of the following ways:

We can do all this if we can find the Entry that we want to change. Specifically, we want the Entry's Position in the heap tree, so that we can bubble it up and down to ancestor and decendant Positions if necessary.

A priority queue that can support these operations is called an "adaptable priority queue" in the textbook. I sometimes call it a "repriority queue," because you can reprioritize its entries.

Searching for the Entry to Change

The main problem is that searching a heap is slow. As we saw in class, it is O(n). If the Entry we we want is not at the root of the heap, we need to search under both children of the root, and so on recursively.

But forget about efficiency for the moment: suppose we don't mind O(n). There's still a problem: how do we know when we've found the desired entry? We can't just search for an existing entry with the right key and value, because the value type might not implement an appropriate equals method.

(We could use the comparator to test keys for equality. But that comparator isn't guaranteed to work for values, which may be of a different type. It would be a nuisance for the user to give us a second comparator that could test values for equality -- and more important, comparing values may be slow or impossible. For example, in Homework 8, each value on our priority queue will be an entire collection of ballots for a candidate. Such large data structures would be slow to compare. In a keyed data structure, it should really not be necessary to compare values -- they are just inert objects attached to the keys, along for the ride.)

A better answer is to hang onto the Entry we want (i.e., keep a pointer to it). If we want to reprioritize or delete that entry later, we can find it in O(n) time by comparing it to all the existing entries in the heap. Each comparison can be done using fast == (not slow equals).

Where would we get a pointer to the Entry? Entries are constructed by the insert(key,value) method. So let's suppose that insert returns the Entry it constructs. So we can do something like this this: 

    Entry e = pq.insert(new Integer(17), new StringBuffer("seventeen"));
      ... 
      // do some other random stuff to the priority queue
      ...
    Position p = pq.find(e);  // finds the current position of e

Answer the following in your Readme file:

  1. How would this find(e) method work, in terms of the HeapPriorityQueue and VectorCompleteBinaryTree classes?

Finding the Entry by Lookup Instead of Search

Now that we have a reasonable interface, let's revisit the speed issue. O(n) is just too slow for finding the entry's position on the heap. What is the point of having fast operations on heap entries (replaceKey and remove are O(log n), and replaceValue is O(1)), if finding the entry to operate on takes O(n) anyway? We would like to find the entry in O(1) time!

A consistent theme in this course has been that you can often trade space to get speed. "If you'll need it later, store it now. It's usually faster to look it up than to compute it." So a natural idea is to use a Dictionary that maps from each Entry to its Position. This indeed takes O(1) time on average.

(But can one really use Entry as a hash key? Yes: it implements both hashCode() and equals() methods inherited from Object. The inherited equals() method is the same as ==, so it compares the memory addresses where two Entrys are stored, which is what we want. The inherited hashCode() method is always designed to give the same hash code to values that equals() says are equal: typically it will hash the memory address where the Entry is stored.)

Answer the following in your Readme file:

  1. The hash table dictionary lets you look up an Entry to find its Position. But existing entries move to different positions as new entires bubble up past them. How could you keep the dictionary up to date as the priority queue changes? (Hint: Each HeapPriorityQueue should now store a CompleteBinaryTree and ... what?)

  2. How would find(e) work using this design?

Finding the Entry by Direct Lookup

But there is a better way! "If you'll need it later, store it now," sure ... but it might make a difference where you store it. Remember that you are already hanging onto the entry (which insert returned) for later lookup. Why not store the entry's position right inside the entry? Then you don't have to look it up; you've already got it! This is faster by a constant factor than using an auxiliary hash table. It is also more space-efficient by a constant factor. And it is certainly simpler.

The diagrams at the end of this page may help you visualize this design.

Answer the following in your Readme file:

  1. Your adaptable heap will now store LocationAwareEntry objects instead of MyEntry objects. The book's LocationAwareEntry inner class extends the MyEntry inner class so that it also stores the entry's current Position. (It still has the key() and value() methods needed to implement Entry, of course, but it has other methods too.)

    As always, existing entries may move to new positions in the heap. How do you keep the LocationAwareEntry objects up to date when they move, so that they always know their Positions? (Check section 7.4 of the textbook if you get stuck, but try to figure it out yourself first.)

Designing the Interface

There is one more step, which is to wrap the whole set of ideas in a nice AdaptablePriorityQueue interface. According to our design above, the user's calls will look something like this:

    Entry e = pq.insert(new Integer(17), new StringBuffer("seventeen"));
      ...
      // do some other random stuff to the priority queue
      ...
    Position p = pq.find(e);   // just returns the position stored inside e, namely
                               // the position ((LocationAwareEntry)e).location()
    pq.replaceKey(p, new Integer(14));  // change the key from 17 to 14
    pq.remove(p);
But there is no reason for the user to have to deal with the intermediate Position. We can redesign the reprioritization methods slightly so the user can just say 
    Entry e = pq.insert(new Integer(17), new StringBuffer("seventeen"));
      ...
      // do some other random stuff to the priority queue
      ...
    pq.replaceKey(p, new Integer(14));  // change the key from 17 to 14
    pq.remove(e);
and the lookup of e's position is handled inside those methods.

Here is the resulting interface:

/** Extends the priority queue interface to support removal
 * and reprioritization of elements.  
 */

public interface AdaptablePriorityQueue extends PriorityQueue { 

  /** Remove an entry, and return that entry (for convenience).
   * Note that you can say, for example,
   *    Entry e = pq.remove(pq.min())
   * which is equivalent to 
   *    Entry e = pq.removeMin();
   */
  public Entry remove(Entry e) throws InvalidEntryException;

  /** Replace the key of the given entry.  
   * Return the old key, for convenience.
   */
  public Object replaceKey(Entry e, Object key) throws InvalidEntryException, InvalidKeyException;

  /** Replace the value of the given entry.
   * Return the old value, for convenience.
   */
  public Object replaceValue(Entry e, Object value) throws InvalidEntryException;
}

Answer the following in your Readme file:

    1. Suppose e is a LocationAwareEntry. What would go wrong if the user called e.setKey(k) rather than pq.replaceKey(e,k)?

    2. Notice that setKey() is a public method of LocationAwareEntry. That's because it has to get called from a class other than LocationAwareEntry (specifically, by HeapAdaptablePriorityQueue's replaceKey method). So what prevents the user from making the bad call in the previous question?

    3. Could the AdaptablePriorityQueue interface be implemented without using location-aware entries? Describe two such implementations. (You should still use a heap. Hint: Both alternatives were suggested in the previous discussion.)

Implementing an Adaptable Priority Queue

Your job in this section is to write a HeapAdaptablePriorityQueue class that extends HeapPriorityQueue and implements the AdaptablePriorityQueue interface.

This should be reasonably straightforward, assuming you understood the previous section well enough to answer its questions correctly. (If you didn't, ask for help.)

We've given you some code to start with.

Hints:

Applying Your Locator-Based Priority Queue to the Election

Elections are newsworthy! The best part of an election is sitting around the TV with your friends, watching your candidate's fortunes lurch up and down as the returns come in. I like to alternately celebrate on chocolate-chip cookies and drown my sorrows in milk.

Using locators, you will now improve your SimpleElection class to obtain a ReportedSimpleElection class. Remember that SimpleElection counted the ballots first and then put the candidates on the heap. That made for a boring election night. This time you will put the candidates on the heap first and then count the ballots. As candidates accumulate votes, their positions on the heap will change.

You will print a news bulletin whenever the front-runner changes, something like this:

Pulling into the lead with 1 of 1 votes is Candidate 1: Born
Pulling into the lead with 2 of 4 votes is Candidate 18: Sullivan
Pulling into the lead with 4 of 17 votes is Candidate 19: Toomey
...
[At the end, you should print the top candidates as before.]

This horse race is actually pretty realistic. The ballots are sorted by polling place, so you can watch as the returns come in from different districts of Cambridge. Within polling place, the ballots are sorted by ballot number, which probably means pretty much chronologically.

Start by copying your SimpleElection class to ReportedSimpleElection. (You will have to hand both in.) Then modify the latter to solve the new problem. The code will be fairly similar, with the biggest change coming to your countVote method (if you have one). Of course you should use a HeapAdaptablePriorityQueue.

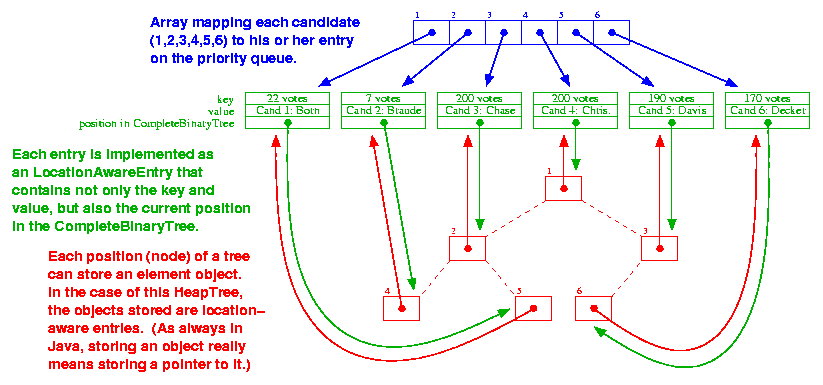
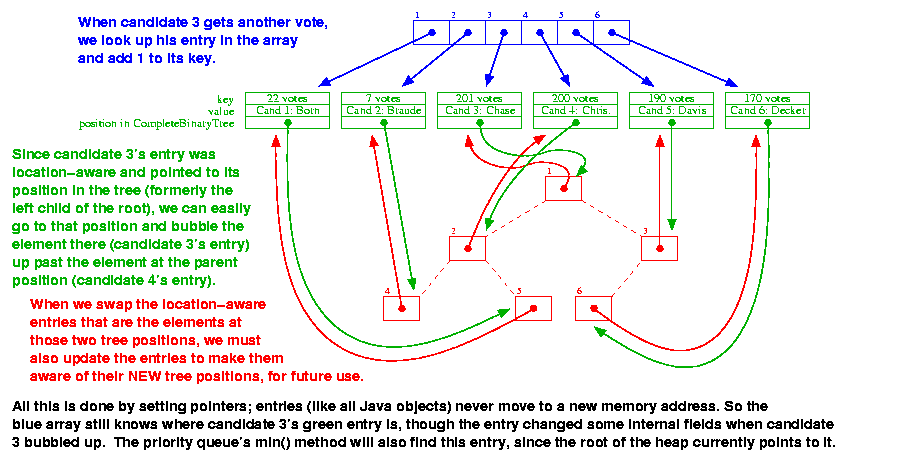
The following diagrams show how the various data structures are laid out in memory, how they interact, and what happens when the front-runner changes. You should often try drawing diagrams like this yourself.

Ballot Reform and Electoral Reform

Coming in Homework 7 and Homework 8!

Jason Eisner - jason@cs.jhu.edu - $Date: 2004/03/18 03:08:38 $