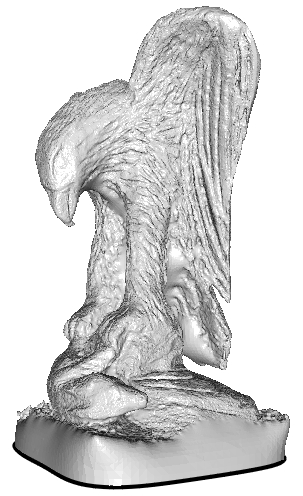
Adaptive Multigrid
This page documents developments on the design and implementation of an adaptive multigrid solver that allows for the efficient solution of Poisson-like systems of equations, discretized over an quad/oct-tree.
This material is based upon work supported by the National Science Foundation under Grant No. 1422325:
- Title: III: CGV: Small: Designing an Adaptive Method for Solving Large Linear Systems of Equations in Two and Three-Dimensional Space
- PI: Michael Kazhdan
- Duration: 09/2014 -- 08/2020
- Students:
- Fabian Prada (Graduated with PhD in December 2018)
- Sing Chun Lee
Goals and Challenges
In numerous fields, ranging from image processing to scientific simulation, solving a large Poisson system is an essential step in integrating locally defined properties into a consistent global solution. Though the linear system is global (with properties at one point in space affecting the solution at points far away), in many cases the details of the solution are only required at particular locations. As a result, computational effort expended on estimating the details of the solution away from these regions of interest is wasted. The proposed research seeks to design, implement, and make publicly available a new solver for addressing this problem - providing a way to adapt traditional hierarchical solvers so that computation is only focused where it is needed.
The motivation for this approach stems from the fact that in solving a Poisson equation, long-distance effects are dominated by lower frequencies, so high-resolution components of the solution need only be computed in regions of interest. Using experiences from prior work in surface reconstruction and large image processing, the PI will explore a modification of traditional multigrid, providing a hierarchical solver even when the function spaces do not nest. To do this the multigrid solver will be modified in two ways. First, to compensate for the fact that the coarser solution cannot be up-sampled to the finer resolutions, the solution of the linear system will be represented as a linear combination of functions at all levels of the hierarchy, not just the finest one. Second, instead of using traditional restriction and prolongation operators to transition between successive levels of the hierarchy, the solver will proceed by iterating through the levels of the hierarchy (fine-to-coarse and then coarse-to-fine as in a typical V- or W-cycle), relaxing the system within each level, and adjusting the constraints at the other levels, accounting for the components of the solution that have already been met. (For example, in the prolongation phase, the coarser solution will be incorporated into the finer levels by adjusting the right-hand-side, rather than updating the current estimate of the solution.) The research will explore both the general design of such a system, as well as domain-specific implementations that facilitate its integration in targeted scientific and entertainment disciplines. Results will be made publicly available in the form C/C++ source code for constructing adapted quadtrees/octrees, formulating the system constraints, and evaluating the computed solution, as well as documentation and application-specific implementations.
Publications, Code, and Presentations
- Accurate Isosurface Interpolation with Hermite Data: [3D Vision, 2015], Code
- Gradient Domain for Color Correction in Large EM Stacks: [ArXiv, 2015], Code
- Fast and Exact (Poisson) Solvers on Symmetric Geometries: [SGP, 2015], Code, Presentation
- Motion Graphs for Unstructured Textured Meshes: [SIGGRAPH, 2016], Code, Presentation
- Field-Aligned Online Surface Reconstruction: [SIGGRAPH, 2017], Code
- Spatiotemporal Atlas Parameterization for Evolving Meshes: [SIGGRAPH, 2017]
- An Adaptive Multigrid Solver for Applications in Computer Graphics: [CGF, 2018], Code
- Gradient-Domain Processing within a Texture Atlas: [SIGGRAPH, 2018], Code
- Möbius Registration: [SGP, 2018], Code
- Dense Point-to-Point Correspondences Between Genus-Zero Shapes: [SGP, 2019], Code
- Poisson Surface Reconstruction with Boundary Constraints: [SGP, 2020], Code
Direct Results
Initial research focuses on extending the cascadic solver used in Poisson Surface Reconstruction. This includes:
- [Version 7.0] Extending the support for function representation/evaluation using the second-order B-spline basis. (This has been used to provide color intepolation support in the context of surface reconstruction.)
|
|
|
| Geometry
| Geometry + Color
|
Notes:
- For performing color interpolation, we "splat" the color values associated with a sample using a kernel whose width is inversely proportional to the sampling density and whose weight is proportional. This provides a color field that adapts to the sampling density and is defined without requiring an explicit solve.
- [Version 8.0] Extending the function representation to B-Splines of different degrees. (This supports a parameterizable trade-off between the accuracy of higher order elements and efficiency/sparsity of linear systems derived from lower order elements.)

| 
| 
| 
| 
|
| Degree: 1
| Degree: 2
| Degree: 3
| Degree: 4
|
| Time: 3.7 s
| Time: 4.9 s
| Time: 9.6 s
| Time: 18.0 s
|
| Memory: 75 MB
| Memory: 141 MB
| Memory: 374 MB
| Memory: 1016 MB
|
| Triangles: 149 K
| Triangles: 148 K
| Triangles: 148 K
| Triangles: 148 K
|
Notes:
- The slightly choppier look of the degree-1 reconstruction may be due to the fact that we cannot use a second-order fit when the implicit function is represented using piecewise trilinear elements.
- Although the system is defined using degree-d elements, the normal field is still represented using second-order elements so that similar constraints are presented to all four systems, and results can be compared more fairly.
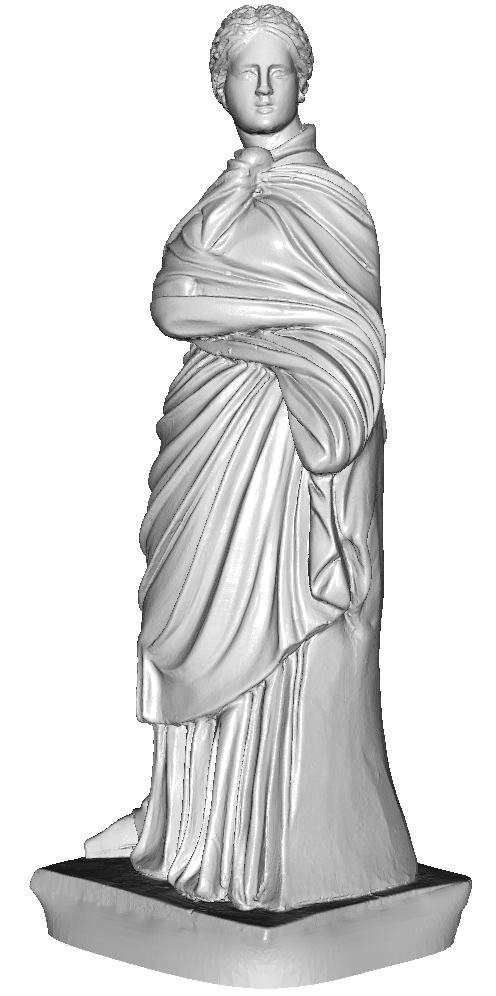
- [Version 9.0] Extending to higher order systems, supporting more general integral and interpolation constraints, and supporting additional boundary conditions. (This enables the implementation of the SSD reconstruction algorithm which uses a bi-Laplacian regularizer using our system, providing a more efficient a less memory intensive solution.)
| 
| 
| 
|
| Poisson Reconstruction
| SSD Reconstruction
(Calakli and Taubin)
| SSD Reconstruction
(Ours)
|
| Time: 110 s
| Time: 354 s
| Time: 92 s
|
| Memory: 2120 MB
| Memory: 6011 MB
| Memory: 2225 MB
|
| Triangles: 4.3 M
| Triangles: 4.0 M
| Triangles: 4.3 M
|
Notes:
- Our SSD implementation turns out to be slightly faster than our implementation of Poisson Reconstruction. This is because the constraints (excepting interpolation) are trivial and do not need to be computed explicitly.
- Initial evaluation indicates that our SSD reconstruction better reproduces some of the detail in the input. This is likely due to the manner in which default parameters are set.
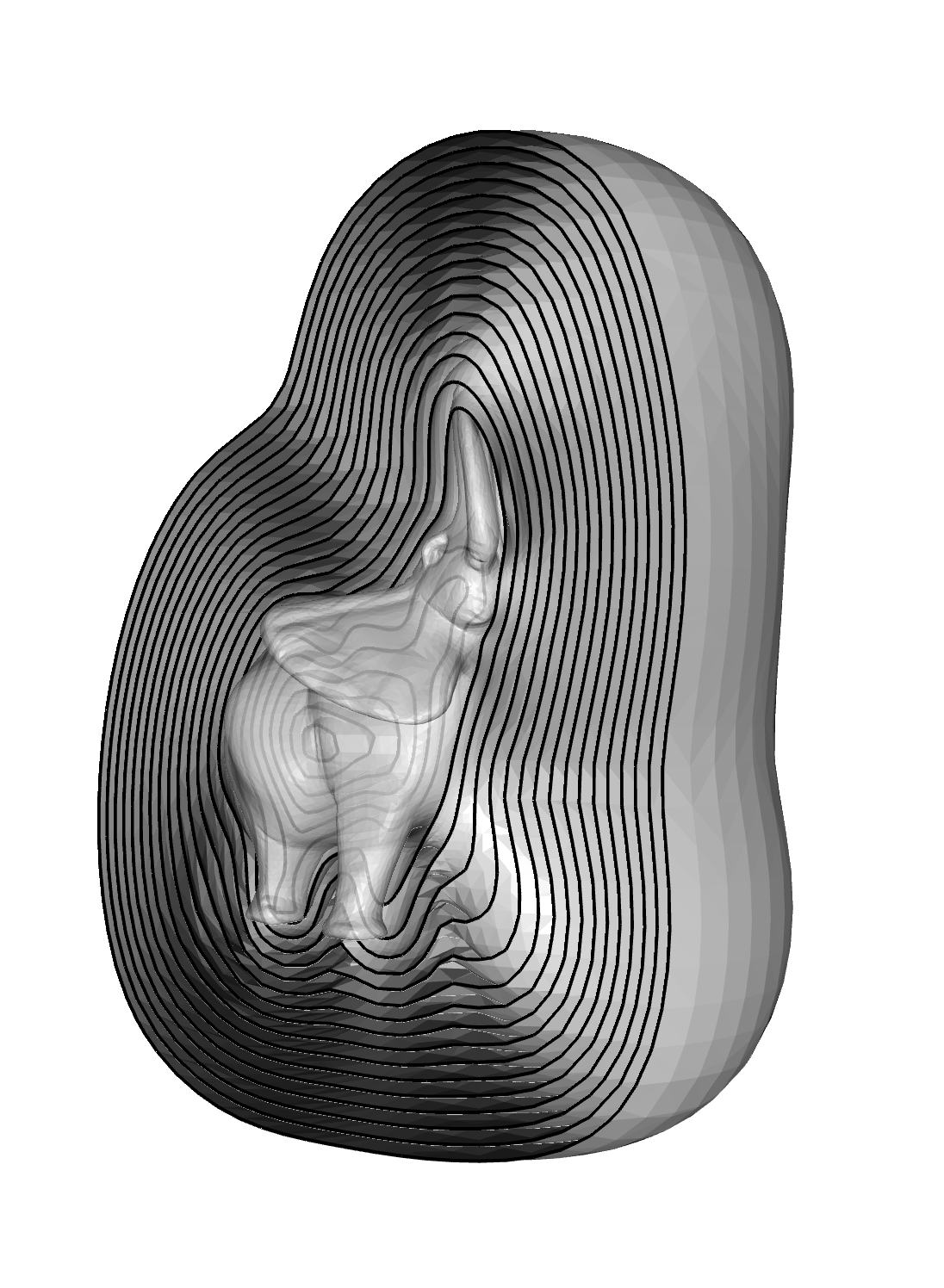
- [Version 10.0] Extension of the cascadic solver to a support arbitrary degree finite-elements in arbitrary dimensions. This enables new applications including quadtree-based gradient-domain image stitching and estimation of the Euclidean Distance Transform using the Heat method.
 |
 |
 |
| Gradient-Domain Stitching (Ours) |
|---|
| Input: 420 MP |
| Time: 47 s |
| Memory: 178 MB |
|

| 
|
| EDT [Saito and Toriwaki, 1994]
| EDT in Heat (Ours)
|
| Time: 78 s
| Time: 14 s
|
| Memory: 8196 MB
| Memory: 346 MB
|
|
- [Version 11.0] Extension of the surface reconstruction code to support the huge (i.e. larger than 2^32-sized) point clouds arrising in geological datasets.
- [Version 12.0] Added support for scattered data (value and/or gradient) interpolation in arbitrary dimensions.
- [Version 13.0] Added the ability to constrain the reconstructed surface to be contained within a prescribed envelope by extending the linear solver to support Dirichlet boundary constraints.
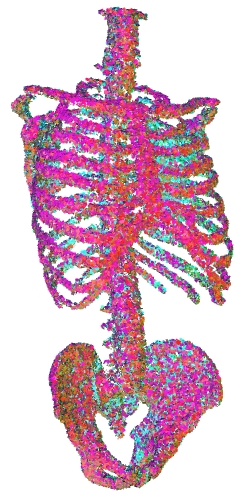 |  | | Input Samples | Constraint Envelope (Depth Hull) |
|---|
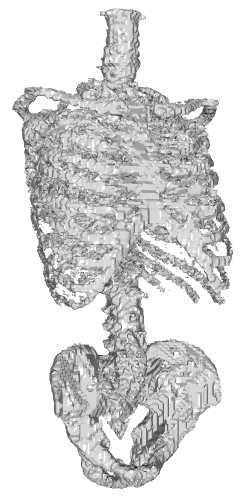
|  | | Reconstruction w/o Envelope |
|---|
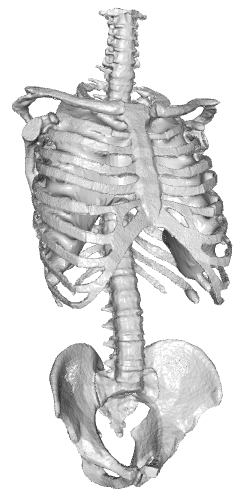
|  | | Reconstruction w/ Envelope |
|---|
|
Indirect Results
- Accurate Isosurface Interpolation with Hermite Data
- This work considers the use of non-linear interpolants for iso-surface extraction (applicable to both reguar grids and adapted octrees) by considering not only the values at the end-points of an edge but also the gradients. This has been shown to be particular valuable for extracing high-quality surfaces when the underlying implicit function fails to be linear near the iso-surface (e.g. for indicator funcionts).
- Gradient Domain for Color Correction in Large EM Stacks
- This work considers the problem of performing gradient domain color-correction on huge (teravoxel) 3D EM data. The processing is decomposed into two phases: An initial smoothing pass to obtain a 3D dataset that is coherent along the z-axis, followed by independent 2D gradient domain fusion to obtain slices that preserve the high-frequency content of the input slices while exhibiting the coherence of the smoothed data. Separating the color correction into these two phases makes the approach trivially parallelizable and provides the space- and time-efficiency required for processing large 3D volumes.
- Fast and Exact (Poisson) Solvers on Symmetric Geometries
- This work considers the problem of solving linear systems on geometries with symmetries. In particular, when the linear system commutes with the symmetry group, the decomposition of the function space into irreducible representations results in a block-diagonalization of the matrix, replacing the solution of one large system with the solutions of many small ones. For Poisson equations on surfaces of revolution, the decomposition into irreducibles is obtained by computing a set of FFTs along the parallels of the surface, and the diagonal blcoks are tri-diagonally banded so that they can be solved in linear time.
- Motion Graphs for Unstructured Textured Meshes
- This work explores extensions of the Poisson equation to applications in vector-field design. Specifically, using the Laplacian of vector-fields as a regularizer, we design a hierarchial optical-flow solver for signals defined on surfaces that do not (directly) support a multi-resolution representation in order to obtain a good (non-local) minimizer to the non-convex and underconstrained optical flow probleem.
- Field-Aligned Online Surface Reconstruction
- This work explores the localization of updates within a hierarchical solver. Applied to the context of surface reconstruction, this allows a user to incrementally add new scans to a 3D reconstruction in time that is proportional to the size of the newly added scan, and independent of the overall size of the model. This, in turn, enables the design of an on-the-fly surface reconstruction system that interactively displays the reconstruction from the current scans and guides the user in choosing locations/orientations for subsequent scans.
- Spatiotemporal Atlas Parameterization for Evolving Meshes
- This work continues the work on "Motion Graphs", leveraging the optical flow solver to refine registration between two surfaces by using the optical flow of textures to constrain the tangential motion of the surface deformation.
- Gradient-Domain Processing within a Texture Atlas
- This work considers the problem of performing signal-processing on surfaces by performing gradient-domain processing directly in the texture domain. Defining a seamless and metric-aware finite-elements system, we show that it possibly to leverage the regularity of the texture domain to design a multigrid solver that supports processing signals over curved geometries at interactive rates.
- Möbius Registration
- This work considers the problem of finding the Möbius registration that best registers two conformal spherical parametrizations. Factoring the group of Möbius transformations into inversions and rotations, we show that individual conformal parametrizations can be cannonically centered with respect to inversions and pairs of conformal parametrizations can be optimally rotationally aligned by leveraging fast signal processing over the sphere and the group of rotations.
- Dense Point-to-Point Correspondences Between Genus-Zero Shapes
- Leveraging our earlier work on Möbius Registration, this work addresses the problem establishing correspondences between similar genus-zero shapes when the deformation taking one shape into the other is not necessarily an isometry. Starting with optimal Möbius alignment, we refine the registration using a novel, efficient, hierarchical, spherical optical flow implementation. Taken in conjunction with a novel flow that transforms the conformal parametrizations into authalic parametrizations, we obtain correspondences that are competitive with state-of-the-art techniques.
Contact Info
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation
Last updated 09/01/2020